Speculative Decoding

Summary.

This paper suggests to use a small approximation model to propose sequences of tokens that will later be checked by a larger model. Larger models can reject the proposal of the smaller model if it deems the generated tokens as unlikely to occur naturally. Overall the sampling scheme works as if we are sampling from the large model directly. This idea works because checking whether a sequence of tokens is likely to occur naturally is much faster than (autoregressive) sampling for the same model.

Discussion.

Sampling scheme. Here we intuitively explain the proposed sampling technique based on the whiteboard drawing of Ani.

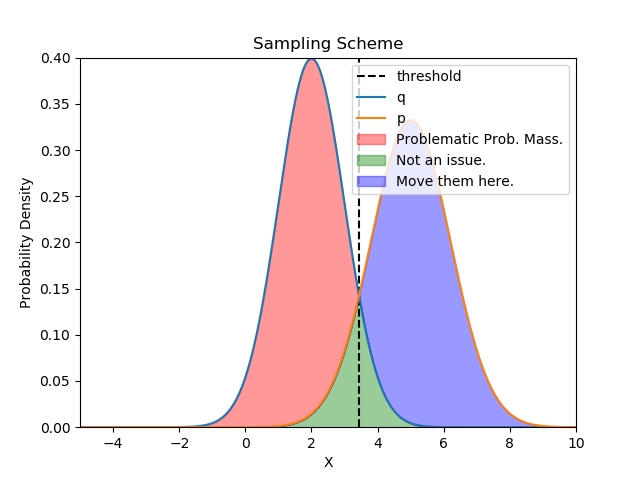
q refers to the pdf (probability density function) of the smaller approximation model, and p the pdf of the larger/original model. We always sample from q, and whenever q(x) < p(x) for a sampled x ~ q, we keep it. This corresponds to the region right to the vertical dashed line labeled “threshold”. However if we end up left to the threshold, this means q(x) > p(x), i.e., the approximation model deems the generated sequence more plausible than the original model does. This is undesirable as we intend to mimic the distribution of p with q. In this case, we accept only with a probability of p(x)/q(x), if rejected, we resample from the blue region (i.e., the distribution after normalizing p(x) - q(x)), essentially favoring the X’s that the original models deems more plausible than the approximation model does.

The gist of the idea is that if we want to approximate p with q, the red region is problematic as sampling from q favors the corresponding X more than p. Similarly, the blue region is problematic as sampling from q omits the corresponding X more than p. We can address this imbalance by “moving” the red probability mass to the blue region with the proposed sampling scheme.

When to speculate? The fact that some sequence of tokens are easier to generate than the other is an observation that motivates this work. However, the proposed sampling scheme does not invoke the smaller model only on easy sequences. One can potentially use signals such as argmax logit magnitude to predict when the smaller models output will be inadequate and therefore ask help from the larger models under such circumstances to prevent wasteful speculation.

Memory access saving. Even though speculative sampling does not decrease the amount of computation required for inference (in fact it will increase it due to running the approximation model), it will significantly reduce the amount of memory access. Here’s why.

• Baseline. Without speculative decoding, a large language model generates one token at a time. For a causal LLM, usually the key/values of previously generated tokens are cached, but we still need to load them from DRAM to register to compute with them every single time we run a forward pass to generate a new token.

• Perfect guesses/zero cost approximation model. To simplify things, let’s consider the memory saving in the context where the approximation model always guesses correctly and costs nothing to run. In this case, to sample the same sequence of tokens, speculative decoding requires exactly the same number of floating point operations as baseline because we need to check all the speculatively generated tokens with the original model. And checking costs as much compute as generation. However the checking is done with a single forward pass. So we only need to load and use cached key/values for previously generated tokens once. This enables memory saving by a factor of $\gamma$, the number of tokens we speculatively generate using the approximation model in a single round.