GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers

Summary. The authors propose a solution to tackle post-training one-shot weight quantization problem for LLMs without retraining. The solution mainly includes a trick to reduce the computational overhead of computing the Hessian inverse of the weight matrices during quantization by reverting a design choice that is insignificant to quantization efficacy from the previous SOTA solution, resulting in asymptotic runtime complexity improvement. The resulting solution can quantize gigantic (175B) LLMs within hours, preserving much of their language modeling/few shots learning ability.

Discussion.

Difficulties of Batching.  One of the central premise of this work is that batching is hard for autoregressive inference. This is central because it implies the problem of autoregressive inference is inherently memory bound, which further implies that saving on memory bandwidth alone will lead to significant speed up. Why is this premise true? We do not see a concrete explanation but speculate there may be the following reasons: 1). Sequence length: often during inference, causal language models may generate texts of different lengths for different prompts, which makes the shape of the input/hidden states tensor as well as associated computation irregular (ragged), making trivial data-parallelism difficult to load-balance. 2). A core benefit of batching is increased memory reuse. For MLP, batching allows the same set of weights to apply to more data; such increased memory reuse reduces memory transfer required to complete inference computation, speeding up memory-bound workloads. However for attention-based models, the computation of K@Q (key & query matrix) entails a distinct pair of matrix K, Q for each inference example, thus no increased re-use across different batches is possible.

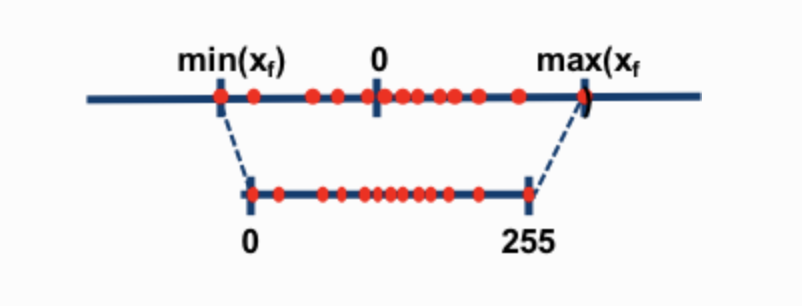
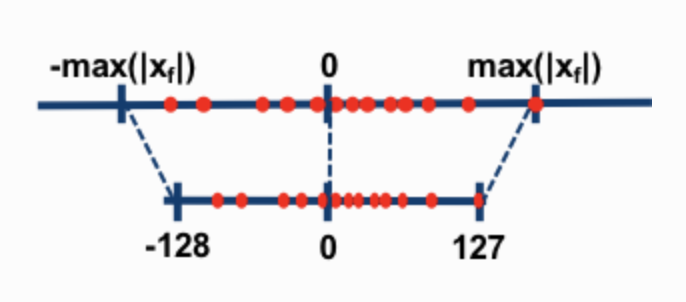
Quantization Setup. GPTQ uses asymmetric quantization, which means that its quantization grid (the discrete set of values on the real number line that can be precisely represented by the quantized integer values) is not centered around zero. On the other hand, the quantization grid of any symmetric quantization technique is centered around zero. The following illustration is taken from Intel Neural Network Distiller and illustrates two schemes with the upper number line representing the un-quantized weight values and lower one representing the quantized weight values. Asymmetric quantization scheme requires more computations than symmetric one during inference, but often incurs less quantization error.

Furthermore, GPTQ also only quantizes weights, but not activation. The reason is likely that weights are static and thus easier to quantize than activation, which is dynamic and dependent on inputs. An implication is that during inference, GPTQ has to multiply floating point activation and integer weights, and no hardware supports such multiplication natively so we do not expect multiplications in GPTQ quantized models to run faster on today’s hardware, though specialized hardware may exist to support this kind of multiplication in the future.

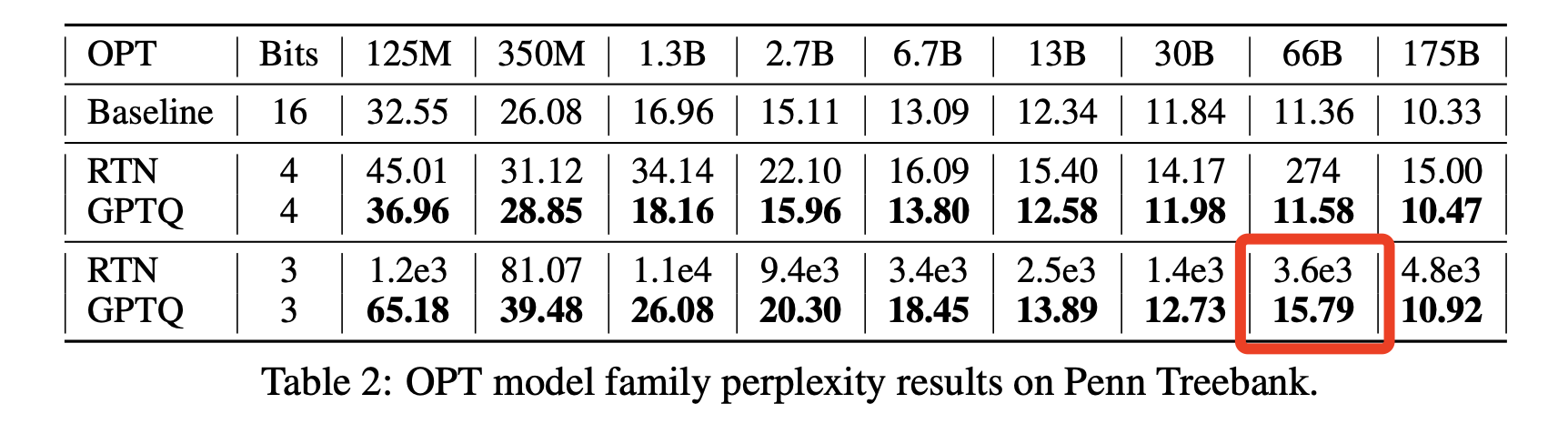
Results. Two interesting results exist in the paper. We don’t find comments in the paper about them. Firstly, OPT-66B models are really unfriendly to quantization. When quantized to 3 bits, it shows a significantly higher perplexity than models with similar size. Interestingly, nothing appears too out of the ordinary when we look at the perplexities of the original, un-quantized models.

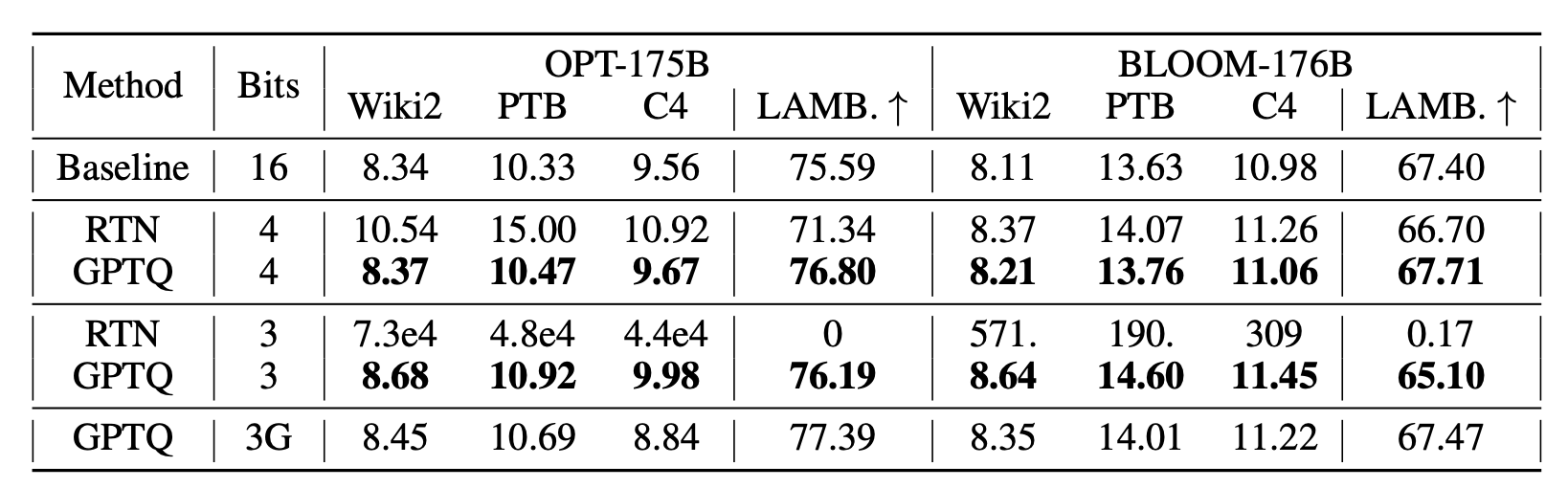
Second observation is that OPT-175B and BLOOM-176B models both show slight improvement on LAMBADA datasets. The objective function being minimized during quantization is the distance between quantized layer output and original layer output. This objective should not improve zero-shot learning abilities.

Cost of Hessian Inverse. We wonder whether the computation of Hessian inverse represents a huge overhead, which requires O(N^3) floating point operations to compute. And during quantization, we need to compute the Hessian inverse for every single layer, some of the larger models can have > 90 layers.

Relation to recent works (contributed by Ani). Activations [quantization] are hard because either you clip to max per channel, and lose all fine grained distinction inside the quantization, or clip to any other metric and lose the outlier activations. Low precision suffers this issue too because the rounding causes massive changes when the activations are highly skewed. Among LLM.int8 [1], SmoothQuant [2], GPTQ, each paper solves this problem differently. LLM.int8 solved it by having a few 16 bit features. SmoothQuant solved it by scaling down outlier activations and scaling up outlier weights to compensate. These two papers do true quantization, and then send the results to 16bit after the matmul is done. GPTQ solves this problem in a different way. They use fake quantization, which is totally fine for this memory/communication bound setting. They essentially distribute the low precision errors throughout the output channels, which allows for the outlier activations to be accurately reconstructed by the rest of the weights.

[1] LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

[2] SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models