Decentralized Training of Foundation Models in Heterogeneous Environments
Paper link: https://arxiv.org/abs/2206.01288
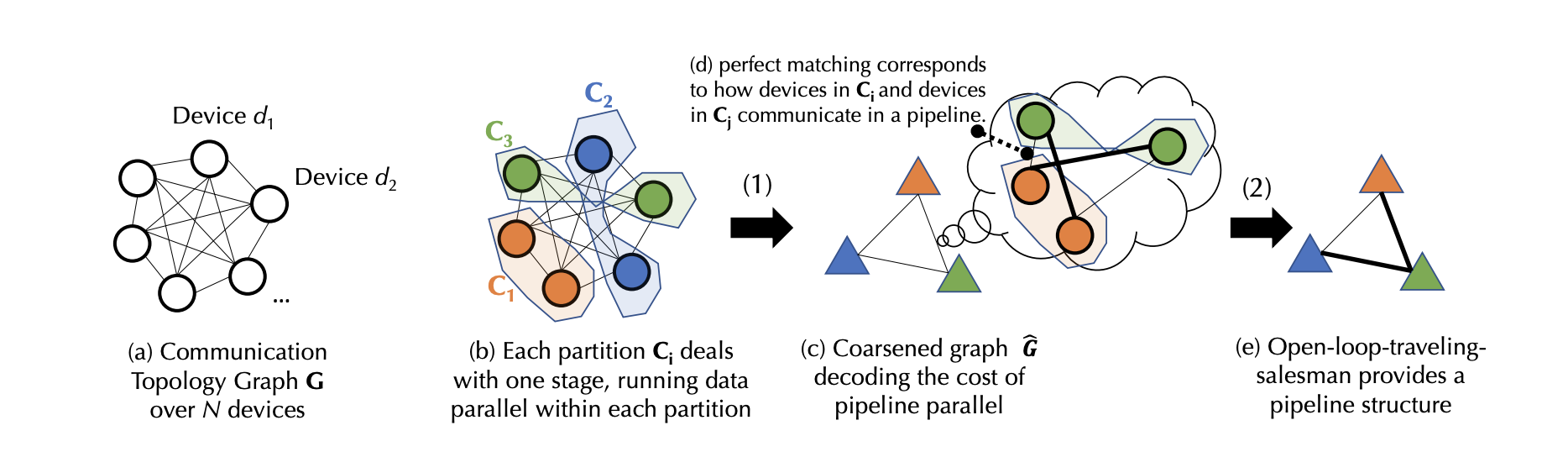
Summary. This paper formalizes the problem of decentralized training in (network-wise) heterogeneous environments. Specifically, the scheduler starts with (a). a communication topology graph describing the communication bandwidth/latency of available devices. Then it proceeds to (b) partition the graph into groups of equal size, denoted as data parallel (DP) groups. Each DP group handles a unique subset of model layers, within which training executes in data-parallel. In (c), nodes within the same group collapse into one node to produce a coarsened communication graph. The scheduler then computes the communication cost between DP groups, should they be assigned consecutive layers that requires communication, and uses them as edge weights in the coarsened graph (d). Finally, in (e) the scheduler figures out optimal assignment of model layers to nodes (DP group) in the coarsened graph.
Discussion.
A Thought Experiment. Can we co-design model & training strategy so as to make decentralized heterogenous training compute bound? Specifically there’re these communication overhead:
- Gradient exchange. We only need to exchange gradient at the end of every mini-batch. If we can make batch size arbitrarily large, we will be able to make the gradient communication overhead arbitrarily small. Note that with gradient accumulation, we can usually execute significantly larger batch size than otherwise possible given the physical memory constraint.
- Activation passing. This communication overhead is proportional to the size of the hidden dimension. However, computation scales proportional to the square of hidden dimension size. By increasing the hidden dimension size compute will grow faster than communication to send and receive activation. Increasing hidden dimension size to large enough value, we will be able to completely hide communication within the computation.
Maximize Utilization. If our model can fit within a single GPU, likely the optimal strategy is to use a single GPU as it avoids all communication cost. However the formalism in this paper would preclude such a solution because the following uniqueness constraints implies that all available nodes must participate in training:

Perhaps it’d be beneficial to maximize utilization of each participating compute node as an extra objective to prevent wasteful parallelization.
Robustness. Another interesting implication of this constraint that all nodes must participate in training is that a single slow node may wreck havoc to cluster performance. Imaging someone joining a V100 cluster with a raspberry pi. It may be interesting to think about other adversarial scenarios that may arise from crowd-sourced training like data poisoning.
Fault Tolerance. It seems straightforward to have some fault tolerance within the proposed system. For one, the fact that training is mostly a sequence of deterministic computational steps means that participating nodes are unlikely to run into consensus issues, and when node rejoins after network failure, the most devastating consequence is just to redo parts of computation. For another, data parallel execution model offers natural replication of model weights. A dropped node can get model weights from peers in the same data parallel group after rejoining.
Architecture Dependence. It seems like the success of the proposed technique is very much predicated on the unique advantages of transformer models:
- Models like GPT are a sequence of identical computation blocks, which makes load balancing easier. Imagine trying to train a ConvNet in a decentralized heterogenous environment, one has to think about how to balance loads across different data parallel groups as layers of ConvNet are of drastically different size.
- By storing a set of weights (K, Q, V projection layers) and transmitting activations, significant computation may ensue (projection + attention). This is again not the case for MLP/ConvNet where typically only a single matmul happens between stored weights and incoming features, and more data is needed to perform any further computation.
Tasklet. How are tasklets created in the first place? The problem of partitioning computation graphs into subgraphs of tasklets seems like a non-trivial problem in and of itself. Seems like the paper is a bit short on details on this.