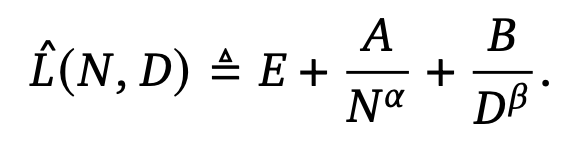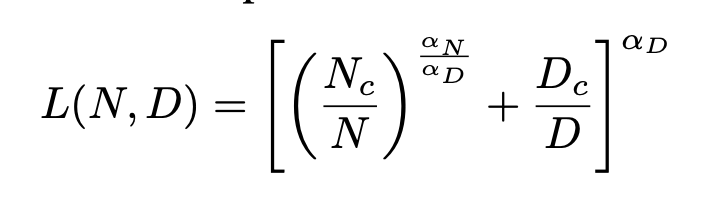Training Compute-Optimal Large Language Models
Summary.
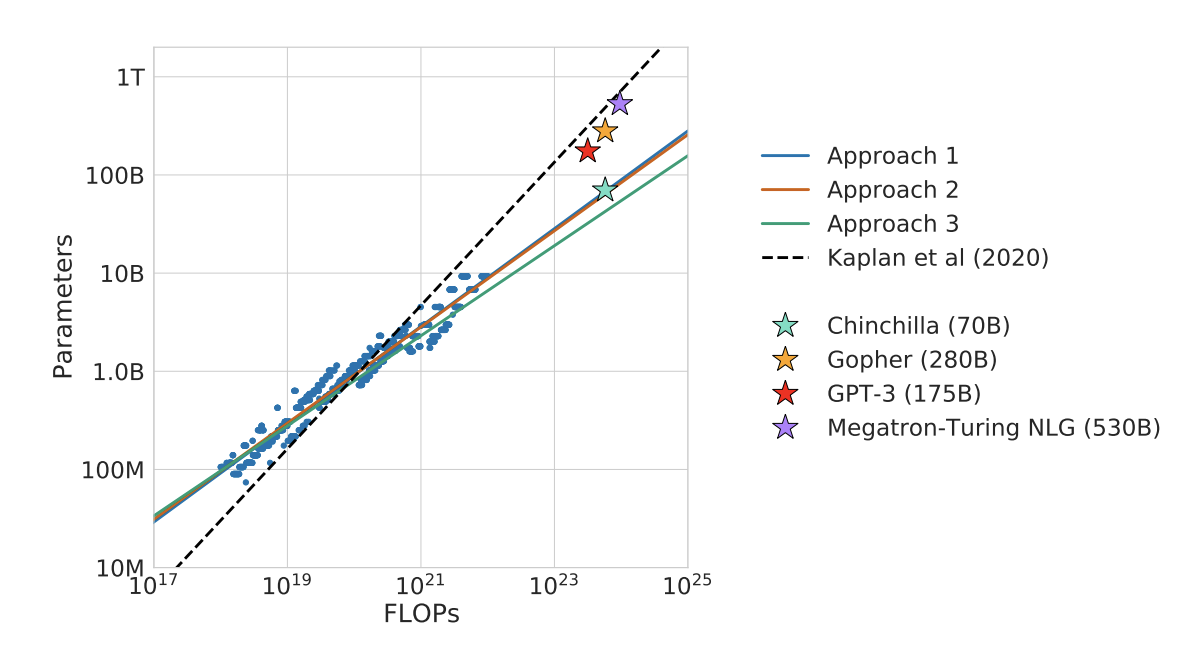
The prevailing wisdom in the large language model community popularized by Kaplan et al. (shown in dashed lines in this plot) is that one need not train a large language model to full convergence to achieve good performance on downstream tasks. An implication of their finding is that, with a fixed increase in computational budget, say 10x, Kaplan et al. recommends increasing the model size by 5.5x and number of training tokens by 1.8x. Several latest large language models including Gopher, GPT-3 and MT NLG followed this prescription and thus fall somewhere near the dashed line.
However, the authors of this paper suggest instead to increase model size and and number of training tokens in similar proportions, which leads to better training result given the same compute budget. The key methodological improvement over Kaplan is that the authors here both varied the training token count and adjusted the learning rate schedule to match the varied training token count. This recommended prescription leads to Chinchilla, which achieves similar performance as more compute intensive models such as Gopher.
Discussion.
Functional form.
We notice that Kaplan et al. and authors of this paper use very different functional forms when fitting empirically derived data points. Specifically, in both functional forms, L(N, D) describes the expected final loss of training a N-parameter transformer model on a dataset with D tokens for 1 epoch. In the equation used in this paper, are parameters to be fitted. We did not attempt to understand the motivation of the complicated functional form used in Kaplan’s work.
The author however gave an informal justification of his particular choice of this functional form, arguing that the three terms in Chinchilla’s power law corresponds to three sources of error:
- A irreducible error corresponding to the loss of Bayes classifier that optimally predicts next token based on the previous sequence of seen tokens, and should correspond to the entropy of natural language.
- An error due to the limitation of the size of the parameter N, which limits our ability to fit the dataset.
- An error due to our imperfect optimization procedure as we only go over the dataset once.
We do not understand why N and D do not interact in multiplicative ways, nor are we aware of a canonical multi-variate power law functional form.
Implication.
This Chinchilla paper is influential and important because the prescription Kaplan gave is essentially to scale up model parameters to a greater extent than dataset size. However, scaling up parameter is detrimental to inference cost during deployment whereas scaling up dataset size has no effect on inference cost. Thus a prescription that advocates for less up-scaling of parameter count, but more up-scaling of dataset size has huge practical implication because it lowers inference cost compared with Kaplan’s prescription.
Sample complexity.
Chinchilla learned from 1.4T tokens, which is way more than what a human being can possibly learn during their lifespan. The latter can be estimated to be << 10 billion tokens for a 20-year-old adult, assuming he/her reads at average speed all the time since birth. This suggests that large language models are still wildly inefficient at learning.
This comparison may however be unfair. Humans may have a superior inductive bias encoded in our genes that facilitates learning. This inductive bias may be “learnt” through evolution by observing a much larger set of training data over many generations of evolution.
Quality of data.
Not all data are the same. It is unclear for the average practitioner who does not have access to DeepMind’s high quality data or their sophisticated data cleansing schemes, how much of the scaling prescriptions in this paper is applicable. Would increasing the training tokens by including garbage data scraped off the Internet help improve the performance of your model? Probably not.