Efficiently Modeling Long Sequences with Structured State Spaces
Summary. The author proposes to use state space model (c.f. below for more detail), a well-known concept in control theory, to handle long range dependencies efficiently, a known shortcoming for RNN/Transformer sequence models. Two key ingredients to make it work in practice - 1). Use Hippo matrix as initialization to facilitate memorization/prevent gradient explosion/vanishing. 2). Efficient parameterization which can convert state space model into a large 1D convolution that allows for efficient parallelization. The benefits include much stronger ability to capture long range dependency, O(1) cost per token for autoregressive generation (as opposed to O(L) for transformers where L is sequence length) and the ability to process continuous but discretized sequence (eg. audio) with different sampling frequency without retraining.
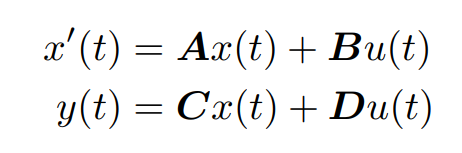
State space model. State space models have the above form. Roughly speaking it maps a 1D input signal u(t) to a N-D hidden states and eventually maps the hidden states back to a 1D output signal y(t). A, B, C, D are all parameter matrices learned through gradient descent.
Discussion.
Hippo Matrix. The following looks important, but what does it mean really:

Looking into [1], we must interpret this statement in the context of online function approximation: Hippo produces operators that optimally maps (and updates) input signals to a set of coefficients of orthogonal polynomial basis online. The optimality of the mapping is defined with respect to specific measures that capture user preference. The hidden states (polynomial basis coefficients) thus stores a summary of the input function.
This motivation makes us wonder whether the proposed Hippo initialization works the best when dealing with continuous signals (audio) and may work as well with discretized tokens (NLP tasks like question answering).
Role of Initialization. A key trick to getting state space model to work is the Hippo initialization, which helps memorize input signals in a compressed form in the hidden states. What role does this Hippo initialization play? If the goal is to memorize inputs, then why bother updating this matrix through gradient descent? If memorization alone is not sufficient to solve long range dependency, what additional mechanisms are desirable/learnt during the training process?
To hypothesize, more data/visualizations would be helpful. Specifically, the paper presents some visualization of the convolutional kernel corresponding to the state space model after training, how does it compare with the same kernel before training at initialization with A initialized to the Hippo matrix?
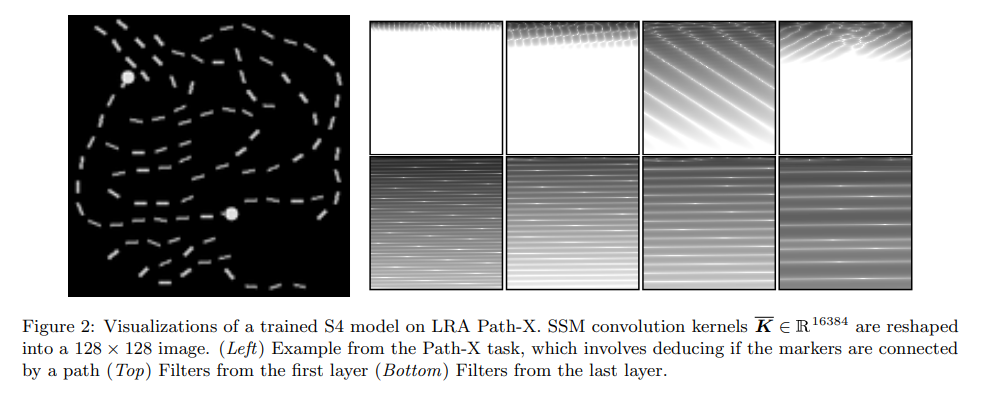
Practical implication. While this paper presents an exciting new set of results, we are unclear whether to use it in our work. There are two additional pieces of information we need to answer this question:
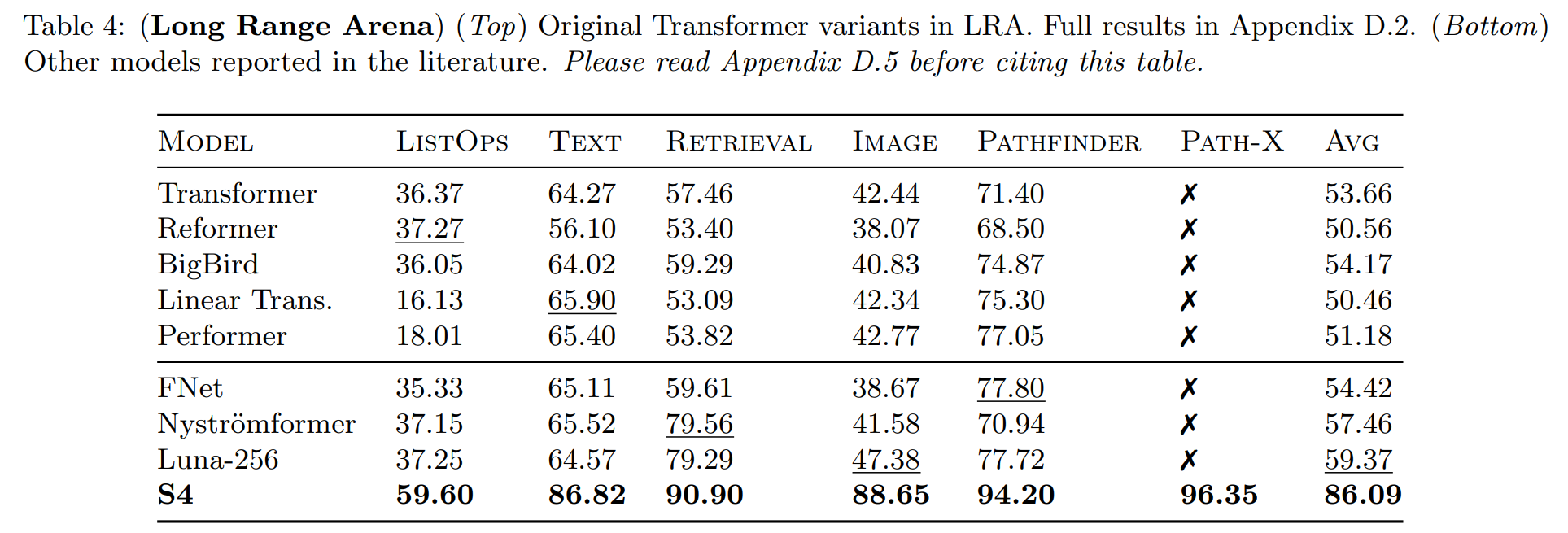
Scaling behavior. When comparing two families of model architecture, say state space model and transformers, it’s important to know if I scale these models up will I get better task performance. However, many comparisons presented in this paper, (c.f. figure below), are point comparisons that does not allow for comparison of scaling behaviors.
Compute normalized performance number. For the figure below, the author controls for the number of parameters when comparing across different architectures. However, in the real world people often care about maximizing accuracy under the same training/inference compute budget. So a more informative set of results will compare performance normalized by the training/inference compute time.
[1] HiPPO: Recurrent Memory with Optimal Polynomial Projections